Búsqueda personalizada

Fórmulas de ordenaciones y combinaciones

Con repetición y con orden.

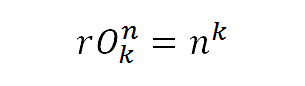
Sin repetición y con orden.

Con repetición y sin orden.

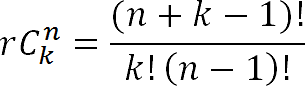
Sin repetición y sin orden.

Ejemplos

Tenemos 5 elementos.

que llamaremos:

A,B,C,D,E

Entonces:

n = 5

k = 3

Si tomamos 3 elementos cada vez con orden y con repetición de 5 elementos tendremos 125 ordenaciones:
Ordenaciones con repeticion de 5 elementos tomando 3 cada vez

Lo calculamos con la fórmula:

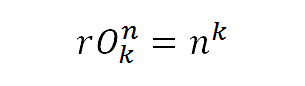
Sustituimos

n= 5 y k = 3

Si tomamos 3 elementos cada vez con orden y sin repetición de 5 elementos tendremos 60 ordenaciones:
Ordenaciones sin repeticion de 5 elementos tomando 3 cada vez

Lo calculamos con la fórmula:

Si tomamos 3 elementos cada vez sin orden y con repetición de 5 elementos tendremos 35 combinaciones:
Combinaciones sin orden y con repeticion de 5 elementos tomando 3 cada vez

Lo calculamos con la fórmula:

Si tomamos 3 elementos cada vez sin orden y sin repetición de 5 elementos tendremos 10 combinaciones:
Combinaciones sin orden y sin repeticion de 5 elementos tomando 3 cada vez

Lo calculamos con la fórmula:

Otros ejemplos

En el juego de “Melate” se eligen 6 de 56 números, no importa el orden de los números y no se eligen números repetidos, por lo que es una combinación de 56 elementos sin orden y sin repetición.

n=56

k = 6

Sustituimos

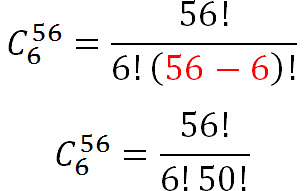
Desarrollamos el 56! hasta 50!

Simplificamos los factores del numerador con los del denominador

Si cada juego cuesta $15,¿ cuanto costaría llenar todas las combinaciones?

Una carrera de 12 caballos en donde apostamos al primero segundo y tercer lugar, esto es con orden y sin repetición, (un caballo no puede ocupar dos o más lugares de llegada)

n=12

k = 3

Sustituimos

Desarrollamos el 12! hasta 9!

Progol es una quiniela de 14 partidos de fútbol soccer nacional e internacional, en la que se debe predecir el resultado (Local, Empate o Visita), ¿ De cuantas formas se puede llenar una quiniela?

Tenemos una ordenación con repetición, en este caso n = 3 (Gana, empata o pierde) mientras que k = 14.

" k" puede ser mayor que "n" debido a que es con repetición.

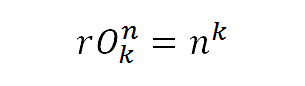
Sustituimos

Otros ejemplos

Calcular las ordenaciones y combinaciones de n = 20 y k = 8.

Con Orden y con repetición.

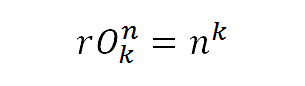
Sustituimos

Con Orden y sin repetición.

Sustituimos

Desarrollamos el 20! hasta el 12!

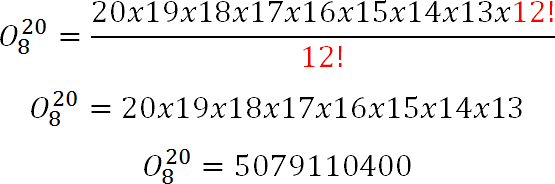
Sin Orden y con repetición.

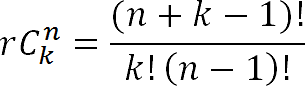
Sustituimos

Desarrollamos el 27! hasta 19!

Desarrollamos el 8 !

Simplificamos los factores del numerador con los del denominador.

Sin Orden y sin repetición.

Sustituimos

Desarrollamos el 20! hasta 12!

Desarrollamos el 8!

Simplificamos los factores del numerador con los del denominador.