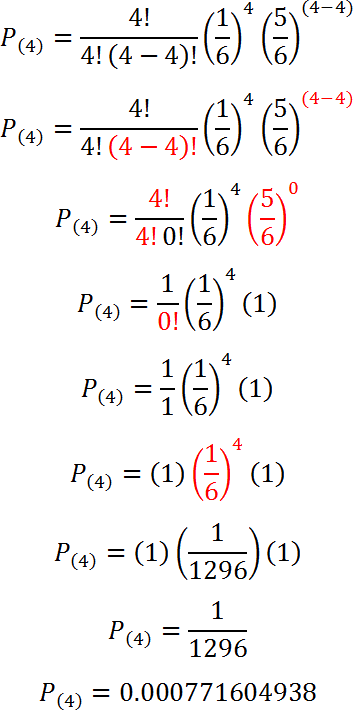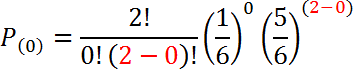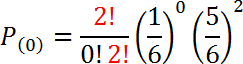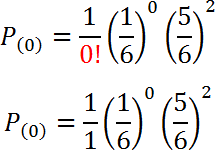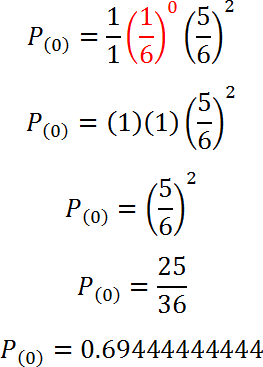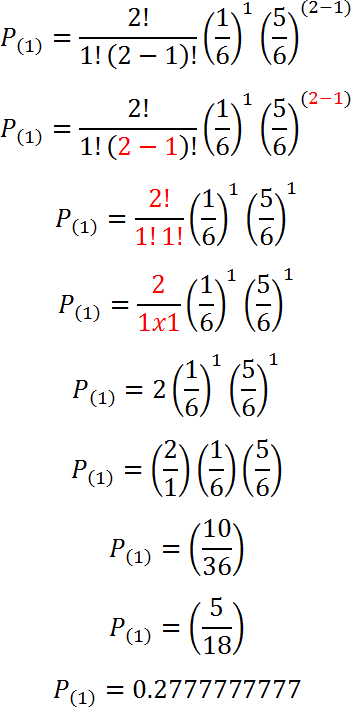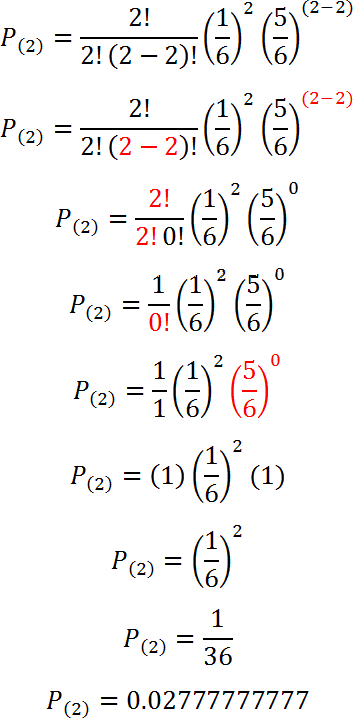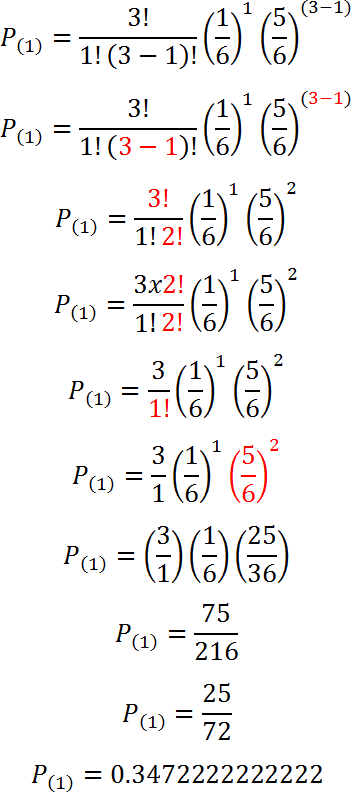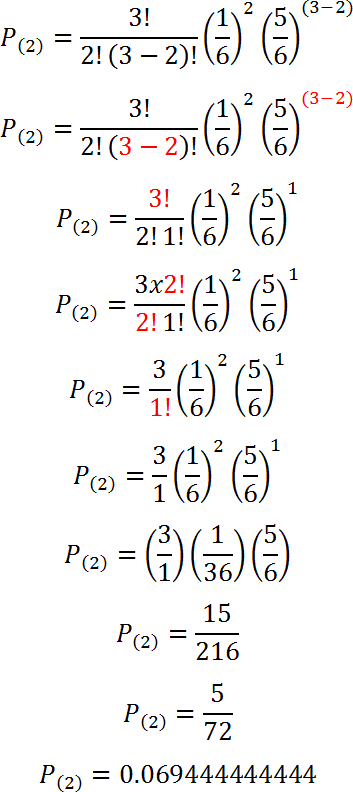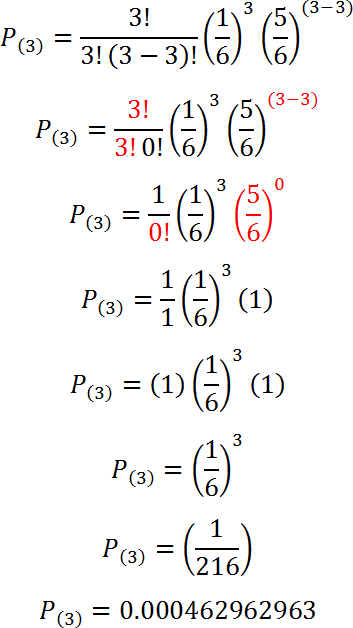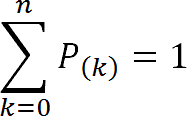Para una distribución de probabilidad binomial, deben darse las siguientes condiciones

En cada prueba del experimento sólo son posibles dos resultados: el suceso "éxito" y su contrario el suceso "fracaso".

El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente, esto es que el valor de la probabilidad de cada prueba no se afecta por pruebas anteriores, ni afecta pruebas futuras.

La probabilidad del suceso "éxito" es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de el suceso "fracaso" es 1- p y la representamos por q .

El experimento consta de un número n de pruebas.

De las "n" pruebas, calculamos la probabilidad de "k" éxitos

Parámetros de la distribución binomial, la media y la desviación estándar.

Ejemplos.

Consideremos el siguiente juego, la apuesta a un número al arrojar un dado. Consideraremos un "éxito" si sale el número que eligimos, y un "fracaso" si sale otro número.

Tenemos que:

p = 1/6

q = 1-p = 5/6

Si hacemos una sola prueba donde P(k) es la probabilidad de k exitos.

tenemos que:

n = 1

P(0) = q = 5/6

P(1) = p = 1/6

Si hacemos dos pruebas, encontraremos lo siguiente:

n = 2

Tendremos cuatro diferentes formas de obtener resultados, estas cuatro formas las vemos en la columna "descripción" de la tabla anterior.

La probabilidad para cada resultado, se calcula multiplicando las probabilidades del resultado de cada prueba, dado que estas son independientes.

El número de "éxitos" lo hacemos contando las "p" de cada línea.

Así podemos calcular la probabilidad desde cero hasta 2 éxitos.

Observa que para la P(1) sumamos dos veces cinco sextos que se encuentran en los renglones verdes de la tabla anterior.

Los resultados en la siguiente tabla.

Podemos poner la probabilidad en decimales.

Y hacemos su gráfica:

Ahora calcularemos lo mismo con la fórmula de distribución binomial.

Sustituimos con n = 2 y k = 0:

2! entre 2! es igual a uno.

Por definición 0! es igual a uno

1/6 elevado a la cero es uno.

Sustituimos con n = 2 y k = 1:

Sustituimos con n = 2 y k = 2:

Que son los mismos valores que obtuvimos de las tablas.

Ahora veamos que pasa si hacemos tres pruebas con el mismo ejemplo de apostar a un número de un dado.

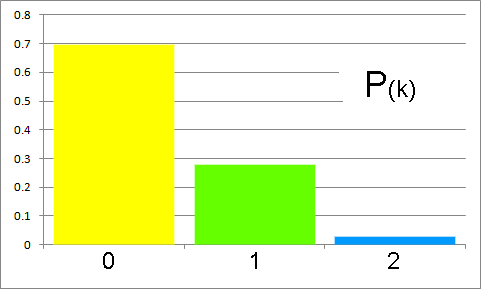
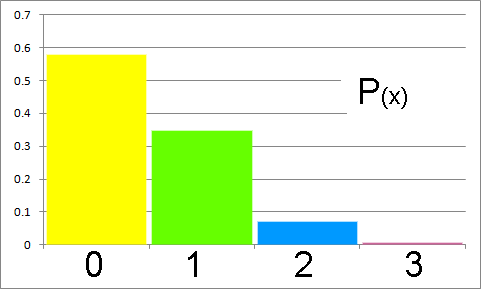
Calculamos los valores de las probabilidades desde cero hasta tres éxitos

Ponemos la probabilidad en decimales.

Y hacemos su gráfica.

Calcularemos ahora las probabilidades de k éxitos para n = 3 con la fórmula binomial.

Para k = 0

Para k = 1

Para k = 2

Para k = 3

Que son los mismos resultados de las tablas.

Hacemos el ejercicio para cuatro pruebas con el mismo ejemplo de apostar a un número al lanzar un dado, observa los colores en la siguiente tabla.

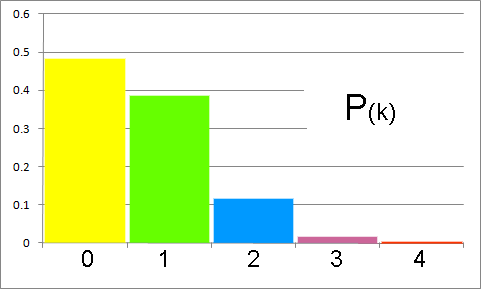
Calculamos los valores de las probabilidades desde cero hasta cuatro éxitos

Ponemos la probabilidad en decimales.

Hacemos la gráfica.

Calcularemos ahora las probabilidades de k éxitos para n = 4 con la fórmula binomial.

Para k = 0

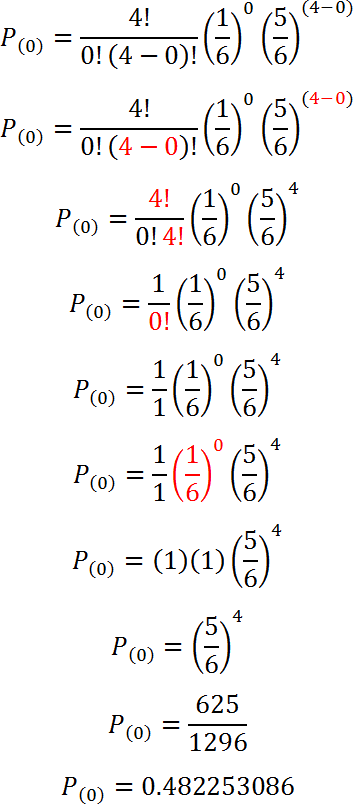
Para k = 1

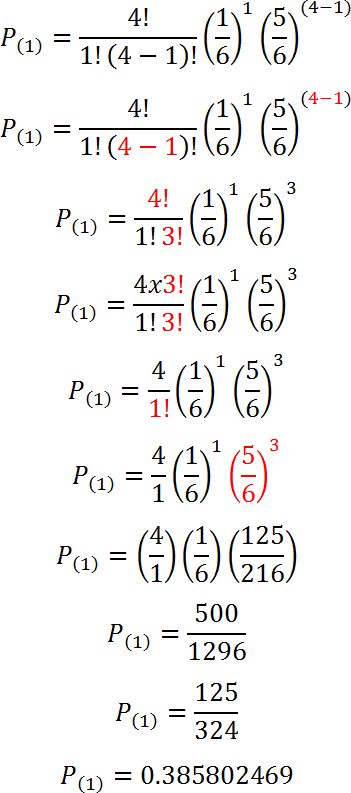
Para k = 2

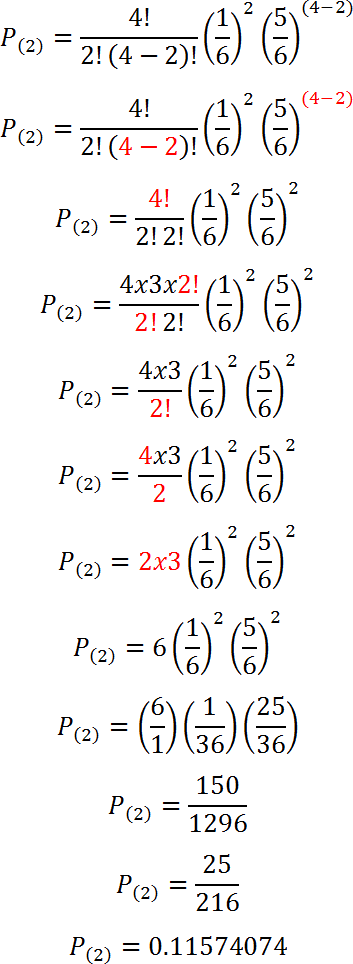
Para k = 3

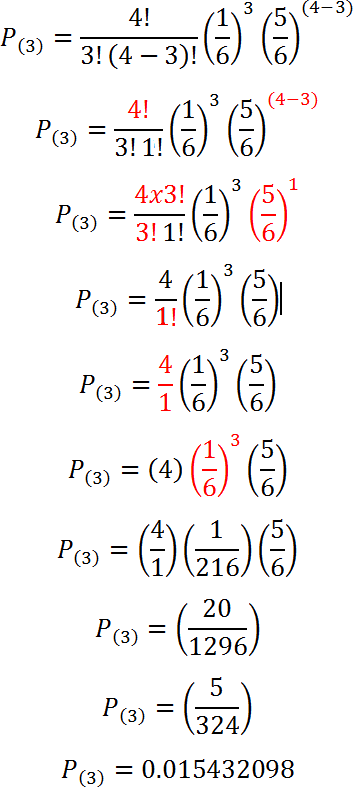
Para k = 4